베이지안 네트워크를 이용한 학습과 행동
(Learning and Acting with Bayes Nets)
인공지능-지능형 에이전트를 중심으로 : Nils J.Nilsson 저서, 최중민. 김준태. 심광섭. 장병탁 공역, 사이텍미디어, 2000 (원서 : Artificial Intelligence : A New Synthesis 1998), Page 371~388
1. 베이지안 네트워크의 학습
베이지안 네트워크 (Bayes network) 를 학습하는 문제는 주어진 평가 척도에 따라 데이터의 훈련 집합 (training set) Ξ 에 가장 잘 부합되는 네트워크를 구하는 것이며, 여기서 Ξ 는 모든 (또는 적어도 몇몇) 변수에 대한 값의 사례 집합이다. 네트워크를 구한다는 것은 DAG (directed acyclic graph, ?방향성 비순환 그래프?) 구조와 DAG 의 각 노드에 연관된 조건부 확률표 (CPT, conditional probability table) 를 함께 구하는 것을 의미한다.
1.1 알려진 네트워크 구조
만일 네트워크의 구조를 안다면 CPT 만을 구하면 되는데 이 경우를 먼저 기술해보자. 전문가들조차도 문제 영역에 맞는 구조만 구하고 CPT 는 얻지 못할 때가 종종 있다. 네트워크 구조를 학습해야 하는 경우에도 CPT 의 학습은 필요하다. CPT 의 학습을 위한 설정에는 간단한 것과 좀 복잡한 것이 있다. 간단한 경우는 결여된 데이터 (missing data) 가 없는 경우이다. 즉, 훈련 집합 Ξ 의 각 요소는 네트워크에 표현된 모든 변수에 대해 값을 가진다. 하지만 보다 현실적인 설정에서는 몇몇 훈련 레코드에 대응값이 없는 변수가 존재할 수 있으며 이러한 결여된 데이터가 CPT 의 학습을 어렵게 만든다.
- 결여된 데이터가 없는 경우
먼저 결여된 데이터가 없다고 가정한다. 훈련 예제가 충분하다면 각 노드와 그 노드의 부모에 대한 표본 통계만 계산하면 된다. 가령 p(Vi) 라는 부모를 가진 노드 Vi 에 대한 CPT 를 구한다고 하자. 앞서의 표기법에 따라 Vi 의 값을 vi 로 나타내자. 노드 Vi 에 대해서는 Vi 가 가질 수 있는 값의 수 (빼기 1) 만큼 테이블이 존재한다. 변수가 부울값으로 표현되는 경우에는 각 노드마다 하나의 CPT 만 존재한다. Vi 가 ki 개의 부모 노드가 있다면 각 부모가 두 값 중 하나를 가지므로, 테이블은 2ki 개의 항목 (행) 을 가진다. Vi 의 부모와 연관된 변수를 벡터변수 Pi 로 나타내고, 이 변수의 값은 값의 벡터인 Pi 로 나타낸다. 표본 통계
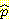 (Vi = vi |Pi = Pi) 는 Vi = vi 이고 동시에 Pi = Pi 를 만족하는 Ξ 의 예제의 수를 Pi = Pi 를 만족하는 예제의 수로 나눈 것이다. CPT 를 학습하기 위해서는 네트워크의 모든 노드에 대해 실제 데이터에 대한 이 표본 통계를 사용하면 된다.
(Vi = vi |Pi = Pi) 는 Vi = vi 이고 동시에 Pi = Pi 를 만족하는 Ξ 의 예제의 수를 Pi = Pi 를 만족하는 예제의 수로 나눈 것이다. CPT 를 학습하기 위해서는 네트워크의 모든 노드에 대해 실제 데이터에 대한 이 표본 통계를 사용하면 된다.
|
G |
M |
B |
L |
사례 개수 |
|
참 |
참 |
참 |
참 |
54 |
|
참 |
참 |
참 |
거짓 |
1 |
|
참 |
거짓 |
참 |
참 |
7 |
|
참 |
거짓 |
참 |
거짓 |
27 |
|
거짓 |
참 |
참 |
참 |
3 |
|
거짓 |
거짓 |
참 |
거짓 |
2 |
|
거짓 |
거짓 |
거짓 |
참 |
4 |
|
거짓 |
거짓 |
거짓 |
거짓 |
2 |
|
|
|
|
|
100 |
그림 1 예제 네트워크와 예제값
한 예제를 통해 이 계산법을 좀더 명확히 설명하고자 한다. 그림 1 은 그림 6 과 같은 구조를 가진 베이지안 네트워크에서 CPT 는 생략하고 다시 나타낸 것이다. 그림에 나타난 대로, G, M, B, L 값을 가진 100 개의 집합을 관찰한다고 하자 (어떤 조합은 나타나지 않기도 하고, 어떤 조합은 다른 것보다 더 자주 나타난다). 예를 들어, 표본 확률  (B = 참) 를 계산하려면 단순히 모든 예제 중에서 B 가 참인 예제의 비율을 계산하면 되며, 따라서
(B = 참) 를 계산하려면 단순히 모든 예제 중에서 B 가 참인 예제의 비율을 계산하면 되며, 따라서  (B = 참) = 0.94 가 된다. 유사한 방법으로 계산하면
(B = 참) = 0.94 가 된다. 유사한 방법으로 계산하면 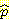 (L = 참) = 0.68 이 된다. B 와 L 노드에 대해 CPT 에는 이들 확률만 저장하면 된다.
(L = 참) = 0.68 이 된다. B 와 L 노드에 대해 CPT 에는 이들 확률만 저장하면 된다.
M 노드에 대한 CPT 행의 계산은 다음과 같은 전형적인 계산법으로 설명하고자 한다. 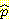 (M = 참 | B = 참, L = 거짓) [줄여서
(M = 참 | B = 참, L = 거짓) [줄여서 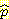 (M | B, ¬L) 로 씀] 를 계산하기 위해 M 이 참이고 B 가 참이고 L 이 거짓인 경우의 수를 세어, B 가 참이고 L 이 거짓인 경우의 수로 나눈다. 이 결과
(M | B, ¬L) 로 씀] 를 계산하기 위해 M 이 참이고 B 가 참이고 L 이 거짓인 경우의 수를 세어, B 가 참이고 L 이 거짓인 경우의 수로 나눈다. 이 결과 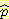 (M | B, ¬L) = 0.03 이 된다. 같은 계산법을 이용해서 G 노드에 대한 CPT 를 구한다. 표본 통계의 모든 집합을 계산해서 그림 6 에 주어진 CPT 와 비교해 볼 수도 있다.
(M | B, ¬L) = 0.03 이 된다. 같은 계산법을 이용해서 G 노드에 대한 CPT 를 구한다. 표본 통계의 모든 집합을 계산해서 그림 6 에 주어진 CPT 와 비교해 볼 수도 있다.
이 예제에서 일부 표본 통계는 매우 작은 수의 예제에만 의존하게 되며, 이 경우 해당되는 확률은 잘못 추측할 수도 있다. 일반적으로 CPT 매개변수가 지수적으로 (exponentially) 커지면 훈련 집합을 통해 매개변수들에 대한 추측을 할 수 있는 능력이 떨어질 수 있다. 이 문제를 줄이려면 많은 매개변수들이 같은 (또는 거의 같은) 값을 가질 가능성을 이용해야 한다. 이 중복성을 이용하여 CPT 에서 계산해야 하는 매개변수의 수를 줄이는 기법이 [Friedman & Goldszmidt 1996a] 에 의해 연구되었다.
CPT 의 항목이 예제를 관찰하기 전에 미리 구한 선험적 확률 (prior probability) 을 가지는 경우도 있다. 주어진 훈련 집합에 대해 CPT 를 베이지안 방법으로 갱신하면 이러한 선험적 확률에 적절한 가중치를 주지만 이 과정은 다소 복잡하다 ([Heckerman, Geiger, & Chickering 1995] 를 참조하라). 아주 큰 훈련 집합에 대해서는 선험적 확률의 효과가 급격히 줄어든다.
- 결여된 데이터가 있는 경우
학습 과정에 이용될 훈련 데이터를 수집할 때 데이터가 빠진 경우가 자주 발생한다. 어떤 때는 있어야 할 데이터가 부주의로 빠지기도 하고, 어떤 때는 데이터가 빠져 있다는 사실 자체가 중요한 경우도 있다. 여기서는 전자의 경우를 다루겠다. [Lauritzen 1991] 은 반복해서 표본 통계를 계산하는 간단하면서 수렴하는 (convergent) 과정을 제시하고, 이 과정이 효과적임을 보였다. 이 방법의 주된 아이디어를 방금 제시한 예제를 가지고 설명하겠다. 가령 그림 1 에 있는 데이터 대신에 다음과 같은 데이터가 있다고 하자.
별표 (*) 는 변수값의 해당 그룹에 대해서 그 위치에 연관된 변수의 값이 없다는 것을 가리킨다. 이제 이러한 네트워크에 대한 CPT 를 계산할 때 결여된 값을 어떻게 다룰 것인가가 문제가 된다. 먼저 G = 거짓, M = 참, L = 참이고 B 는 값이 없는 세 개의 예제를 살펴보자. 이 3 개의 예제 각각은 B = 참이나 B = 거짓 중 하나를 가질 수 있지만 둘 중 어떤 것인지는 모른다. 하지만 이 예제에 대한 G, M, L 의 값은 알고 있으므로, B 값을 모르더라도 G, M, L 이 주어졌을 때의 B 의 확률인
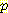 (B | ¬G, M, L) 에 가중치를 준 것이고 다른 하나는 B = 거짓일 때
(B | ¬G, M, L) 에 가중치를 준 것이고 다른 하나는 B = 거짓일 때 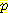 (¬B | ¬G, M, L) = 1 -
(¬B | ¬G, M, L) = 1 - 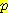 (B | ¬G, M, L) 에 가중치를 준 것이다. (그런데, 그림 1 에서는 G 와 M 이 주어졌을 때 B 가 L 에 조건부 독립적이므로
(B | ¬G, M, L) 에 가중치를 준 것이다. (그런데, 그림 1 에서는 G 와 M 이 주어졌을 때 B 가 L 에 조건부 독립적이므로 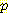 (B | ¬G, M, L) =
(B | ¬G, M, L) = 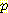 (B | ¬G, M) 이 된다.)
(B | ¬G, M) 이 된다.)
|
G |
M |
B |
L |
사례 개수 |
|
참 |
참 |
참 |
참 |
54 |
|
참 |
참 |
참 |
거짓 |
1 |
|
* |
* |
참 |
참 |
7 |
|
참 |
거짓 |
참 |
거짓 |
27 |
|
거짓 |
참 |
* |
참 |
3 |
|
거짓 |
거짓 |
참 |
거짓 |
2 |
|
거짓 |
거짓 |
거짓 |
참 |
4 |
|
거짓 |
거짓 |
거짓 |
거짓 |
2 |
위와 같은 과정을 B = 참, L = 참이고 G 와 M 의 값이 없는 7 개 예제에 적용하고자 한다. 각 예제는 (G, M) ; (G, ¬M) ; (¬G, ¬M) 의 조합에 해당하는 4 개의 가중치 예제로 바뀌고 각각에 대해 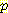 (G, M | B, L),
(G, M | B, L), 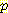 (G, ¬M | B, L),
(G, ¬M | B, L), 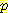 (¬G, M | B, L),
(¬G, M | B, L), 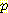 (¬G, ¬M | B, L) 의 확률을 가중치로 준다. 이 확률을 계산하기 위해 다시 한번 네트워크 구조와 CPT 를 이용할 수 있다 (여기서 어느 한 예제라도 결여된 값의 수가 커지면 예제가 지수적으로 증가할 위험이 있다는 것을 알 수 있다).
(¬G, ¬M | B, L) 의 확률을 가중치로 준다. 이 확률을 계산하기 위해 다시 한번 네트워크 구조와 CPT 를 이용할 수 있다 (여기서 어느 한 예제라도 결여된 값의 수가 커지면 예제가 지수적으로 증가할 위험이 있다는 것을 알 수 있다).
이제, 가중치 예제 (결여된 값들이 모든 가능한 방법으로 채워진 예제) 와 그 외 나머지 예제 (결여된 값이 없는 예제) 를 함께 이용해서 빈도 수를 구하여 이것으로부터 CPT 의 근사치를 구할 수 있다. 이 과정은 결여된 값이 없는 경우와 같으며 단지 빈도 수가 (가중치 때문에) 정수가 아닐 수 있다는 것만 예외가 된다. 전에 언급한 대로 확률 추론에 의해 가중치를 계산하기 위해서는 CPT 가 필요하지만 아직 CPT 를 구하지 않은 상태이다. CPT 의 집합에 초점을 맞추기 위해 [Dempster, Laird, & Rubin 1977] 에서 제안된 예상치 최대화 (expectation maximization, EM) 방법을 사용할 수 있다. 먼저 전체 네트워크에 대한 CPT 에 있는 매개변수에 대해서 무작위값을 선택한다. 이 무작위값을 이용해서 필요한 가중치 (관찰된 데이터의 값이 주어졌을 때 결여된 데이터 값의 조건부 확률) 를 계산한다. 다시 이 가중치를 이용해서 새로운 CPT 를 구한다. 이 과정을 CPT 가 수렴할 때까지 반복한다. 대부분의 문제에서 수렴은 매우 빨리 이루어진다.
EM 방법의 적용은 확률 추론을 수행하고 빈도 수를 구하는 컴퓨터 프로그램에 맡기는 것이 가장 현명하다. 앞의 예제와 같이 결여된 값을 가진 소규모의 예제라도 아주 지루한 계산을 필요로 할지 모른다.
1.2 네트워크 구조의 학습
네트워크 구조가 알려져 있지 않으면 훈련 데이터에 가장 적합한 구조와 연관된 CPT 를 찾아야 한다. 이를 위해서는 후보 네트워크를 평가할 척도가 필요하고, 가능한 구조를 탐색하는 프로시저를 명시해야 한다. 이 두 가지를 이 절에서 다루고자 한다.
- 평가 척도
경쟁적인 네트워크를 평가할 때 여러 척도가 사용될 수 있다. 그 중 하나는 코드길이 (description length) 에 기반을 둔 것인데, 이 코드길이의 아이디어는 다음과 같다. 가령 훈련 집합 Ξ 를 누군가에게 전달한다고 하자. 이를 위해서 변수의 값을 비트의 문자열로 코드화할 것이다. 이때 몇 비트가 필요한가? 즉, 메시지의 길이는 얼마인가? 효율적인 코드는 전송될 데이터가 가진 통계적 특성의 이점을 잘 활용하므로, 이 통계적 특성을 베이지안 네트워크로 모델링하려고 한다. 적절한 베이지안 네트워크를 구한 후에는 이 네트워크를 기초로 한 허프만 코드 (Huffman code) 를 이용해서 전송될 데이터를 코드화할 수 있다. 베이지안 네트워크 B 에 의해 주어진 결합 확률 (joint probability) 에 따라 분포된 데이터 집합 Ξ 를 가장 최적으로 코드화하기 위해서는 다음과 같이 L(Ξ, B) 개의 비트가 필요하다는 것이 정보론 (information theory) [Cover & Thomas 1991] 에서 제시되었다.
L(Ξ, B) = -log
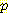 [Ξ]
[Ξ]여기서,
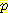 [Ξ] 는 전송되는 특정 데이터의 (B 에서 규정한 결합 분포에 따른) 확률이다. 주어진 특정 데이터 Ξ 에 대해 L(Ξ, B) 를 최소화하는 네트워크 B0 를 구하면 된다. 이 접근 방법에 대한 결론을 맺기 전에 먼저 log
[Ξ] 는 전송되는 특정 데이터의 (B 에서 규정한 결합 분포에 따른) 확률이다. 주어진 특정 데이터 Ξ 에 대해 L(Ξ, B) 를 최소화하는 네트워크 B0 를 구하면 된다. 이 접근 방법에 대한 결론을 맺기 전에 먼저 log 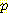 [Ξ] 를 계산하자. 데이터 Ξ 가 m 개의 예제 v1, ..., vm 으로 구성된다고 가정하자. 이때 각 v1 는 n 개 변수의 값에 대한 n 차원의 벡터이다. 그러면
[Ξ] 를 계산하자. 데이터 Ξ 가 m 개의 예제 v1, ..., vm 으로 구성된다고 가정하자. 이때 각 v1 는 n 개 변수의 값에 대한 n 차원의 벡터이다. 그러면  [Ξ] 는 결합 확률
[Ξ] 는 결합 확률  [v1, ..., vm] 이 된다. 각 데이터가 B 에 의해 명시된 확률 분포에 따라 독립적으로 제공된다고 가정하면 다음 두 식을 얻을 수 있다.
[v1, ..., vm] 이 된다. 각 데이터가 B 에 의해 명시된 확률 분포에 따라 독립적으로 제공된다고 가정하면 다음 두 식을 얻을 수 있다. (Ξ) =
(Ξ) = 
 (v1)
(v1)-log
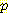 (Ξ) =
(Ξ) =  log
log 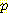 (v1)
(v1)여기서 각
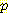 (v1) (변수들이 에서 명시된 값을 가질 결합 확률) vi 는 베이지안 네트워크인 B 로부터 계산된다. 이 계산은 지루하긴 하지만 여러 베이지안 네트워크롤 평가하는데 확실히 이용될 수 있다. 물론 각 네트워크는 네트워크 그래프 구조와 CPT 를 모두 포함한다. 네트워크 구조와 훈련 집합 Ξ 가 주어졌을 때 L(Ξ, B) 를 최소화하는 CPT 는 Ξ 에서 계산된 표본 통계로부터 구한 것이다 [Friedman & Goldszmidt 1996a].
(v1) (변수들이 에서 명시된 값을 가질 결합 확률) vi 는 베이지안 네트워크인 B 로부터 계산된다. 이 계산은 지루하긴 하지만 여러 베이지안 네트워크롤 평가하는데 확실히 이용될 수 있다. 물론 각 네트워크는 네트워크 그래프 구조와 CPT 를 모두 포함한다. 네트워크 구조와 훈련 집합 Ξ 가 주어졌을 때 L(Ξ, B) 를 최소화하는 CPT 는 Ξ 에서 계산된 표본 통계로부터 구한 것이다 [Friedman & Goldszmidt 1996a].하지만 L(Ξ, B) 는 아크가 많은 대규모 네트워크일수록 더 후한 점수를 주기 때문에 이것만으로는 아주 좋은 평가 척도가 되지 못한다. 이러한 네트워크는 너무 Ξ 에만 잘 맞도록 특수화될 수 있다. 즉, 이 데이터에 과다 학습된 결과가 된다. 평가 척도를 적절히 조정하려면, B 에 기반을 둔 효율적인 코드를 이용해서 Ξ 를 누군가에게 전송하기 위해서는 수신자가 메시지를 해독할 수 있도록 B 에 대한 코드 (description) 를 같이 전송해야 한다는 것을 깨달아야 한다. 따라서 L(Ξ, B) 에 항을 하나 추가해야 하는데 이 항은 B 를 전송하는 데 필요한 메시지의 길이가 된다. 개략적으로 말하면 B 를 전송하는 데 필요한 비트수는
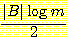 이며, 여기서 |B| 는 B 에 있는 매개변수의 개수이고
이며, 여기서 |B| 는 B 에 있는 매개변수의 개수이고 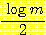 은 일반적으로 각 숫자 매개변수를 나타내기 위해 적절한 비트 수로 간주되고 있다. 조정된 평가 척도 L'(Ξ, B) 는 다음과 같다.
은 일반적으로 각 숫자 매개변수를 나타내기 위해 적절한 비트 수로 간주되고 있다. 조정된 평가 척도 L'(Ξ, B) 는 다음과 같다.L'(Ξ, B) =
 log
log  (vi) +
(vi) + 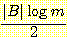
이제 데이터와 네트워크 모두를 코드화할 때 최소 코드길이 (minimum description length) 를 제공하는 네트워크를 구하고자 한다. 이 두 계수를 사용해서 데이터와 네트워크를 모두 전송할 때 알맞은 절충을 할 수 있다.
예를 들어 그림 6 에 있는 네트워크에 대해서 그림 1 에 있는 데이터를 보내기 위한 L'(Ξ, B) 를 계산해 보자. 먼저, 그림 1 의 데이터를 전송하는 데 필요한 비트 수인 L(Ξ, B) 를 계산한다. 이때 이 데이터는 그림 6 에 있는 베이지안 네트워크에 의해 주어진 확률 분포로부터 얻어진다고 가정한다. 그림 1 의 테이블에 있는 첫째 항목을 (first entry) 의 확률은 다음과 같다.
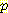 (first entry) =
(first entry) = 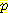 (G | B)
(G | B) 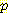 (M | B, L)
(M | B, L) 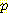 (B)
(B) 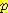 (L)
(L)
= 0.95 × 0.9 × 0.95 × 0.7 = 0.569(밑이 2 인) 음수 로그를 취하면 다음과 같이 된다.
-log
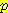 (first entry) = 0.814
(first entry) = 0.814이 데이터에 "첫째 항목" 이 54 개가 있으므로 이들의 L(Ξ, B) 에 대한 기여도는 54 × 0.814 = 43.9 가 된다. 테이블의 다른 항목에 있는 데이터의 기여도는 가각 6.16, 27.9, 52.92, 16.33, 12.32, 24.83, 12.32 이다. 이 기여도값을 더하면 다음과 같이 된다.
L(Ξ, B) = 196.68 비트
다음으로 그림 6 의 네트워크를 전송하기 위해 필요한 비트 수인
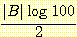 을 계산한다. 이 네트워크에는 8 개의 매개변수가 있으므로 다음과 같이 계산된다.
을 계산한다. 이 네트워크에는 8 개의 매개변수가 있으므로 다음과 같이 계산된다.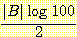 = 4 × 6.64 = 26.58 비트
= 4 × 6.64 = 26.58 비트따라서 이 네트워크에 대한 평가 척도는 다음과 같다.
L'(Ξ, B) = 196.68 + 26.58 = 223.26 비트
다른 네트워크도 같은 방법으로 평가할 수 있다. 아마도 그림 6 에 있는 것이 거의 최적일 것이다.
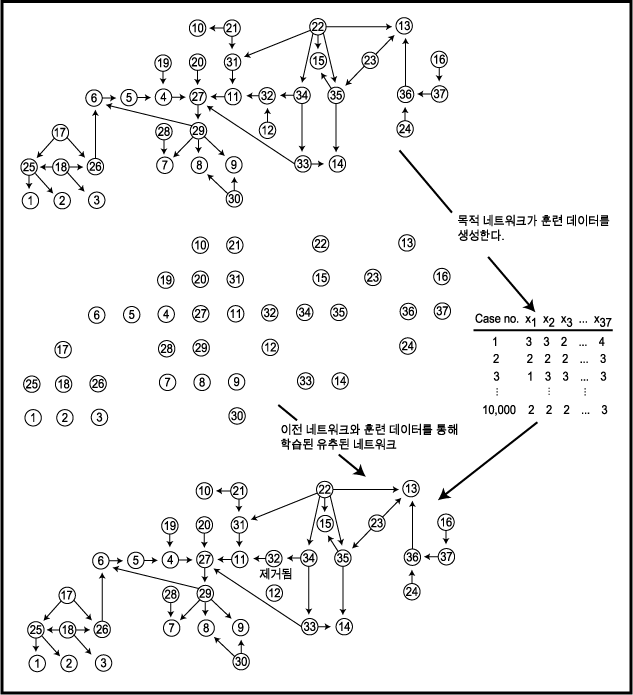
그림 2 네트워크 학습에 대한 실험
- 네트워크 공간의 탐색
가능한 모든 베이지안 네트워크의 집합은 너무 크기 때문에 L'(Ξ, B) 을 최소화하는 네트워크를 구하기 위해 완전 탐색 (exhaustive search) 을 하는 것은 생각할 수조차 없다. 따라서, 언덕 내려오기 (hill-descending) 나 탐욕 (greedy) 탐색과 같은 방법을 이용해서 처음에 주어진 네트워크 (모든 변수가 독립적이라고 가정하며, 예를 들어 아크가 하나도 없는 네트워크) 에 대해서 L'(Ξ, B) 를 계산하고 네트워크를 조금씩 변경시켜 L'(Ξ, B) 가 감소되는지 살펴보는 것이 가능할 것이다. 네트워크를 조금씩 변경시킨다는 것은 아크를 하나 추가 또는 삭제하거나 한 아크의 방향을 반대로 하는 것을 말한다. 변화가 일어날 때마다 Ξ 로부터 유추된 표본 통계를 이용해서 변경된 네트워크의 CPT 를 계산한다. 이 CPT 들은 다시 L'(Ξ, B) 의
 log
log 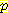 (vi) 항을 계산하는 데 이용된다. 새로운 네트워크의 매개변수 개수는
(vi) 항을 계산하는 데 이용된다. 새로운 네트워크의 매개변수 개수는 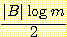 항을 계산하는데 이용된다. 이러한 계산은 코드길이의 계산이 네트워크에 있는 각 CPT 에 대한 계산으로 분해 가능 (decomposable) 하다는 사실을 이용하면 간단해질 수 있다. 평가 척도가 분해 가능하다면 총 척도는 지역 척도의 합이 될 것이다 [Friedman & Goldszmidt 1996a]. 따라서 아크가 추가, 삭제되거나 방향이 반대로 될 때 표본 통계의 변화와 그 변화에 참여한 노드 Vi 에 대한 확률
항을 계산하는데 이용된다. 이러한 계산은 코드길이의 계산이 네트워크에 있는 각 CPT 에 대한 계산으로 분해 가능 (decomposable) 하다는 사실을 이용하면 간단해질 수 있다. 평가 척도가 분해 가능하다면 총 척도는 지역 척도의 합이 될 것이다 [Friedman & Goldszmidt 1996a]. 따라서 아크가 추가, 삭제되거나 방향이 반대로 될 때 표본 통계의 변화와 그 변화에 참여한 노드 Vi 에 대한 확률 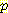 (vi |
(vi | 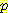 (vi)) 만을 계산하면 된다. 다른
(vi)) 만을 계산하면 된다. 다른  (vi |
(vi | 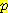 (vi)) 값들은 변하지 않는다. 네트워크가 데이터에 얼마나 적합한지를 평가하는데 코드길이 외에도 다른 분해 가능한 척도가 사용되었다 ([Heckerman, Geiger, & Chickering 1995] 를 참조하라).
(vi)) 값들은 변하지 않는다. 네트워크가 데이터에 얼마나 적합한지를 평가하는데 코드길이 외에도 다른 분해 가능한 척도가 사용되었다 ([Heckerman, Geiger, & Chickering 1995] 를 참조하라).베이지안 네트워크의 학습 방법은 몇몇 중요한 문제에 대한 네트워크 구조나 CPT 를 학습하는 데 이용되었다. 예를 들어, 그림 2 의 네트워크를 고려해 보자. 여기서는 세 개의 네트워크를 나타내었다. 첫 번째 것은 병원의 중환자실의 통풍관리에 사용되는 알람 시스템에 관한 문제에서 37 개의 변수간의 관계를 코드화한 네트워크이다. 이 알려진 네트워크는 37 개의 노드에 대한 10,000 개 크기의 무작위값 (random value) 의 훈련 집합을 생성하기 위해 사용되었다. 이 무작위 예제를 이용하고 두 번째 네트워크 (의존성이 없는 네트워크) 로부터 출발하여 앞에서 기술한 방법을 적용시켜 세 번째 네트워크를 학습하였다 (자세한 사항은 [Spirtes & Meek 1995] 를 참조하라). 자세히 살펴보면 첫 번째 네트워크와 세 번째 네트워크가 단지 한 개의 아크가 빠져 있다는 것만 제외하면 아주 비슷한 구조인 것을 알 수 있다.
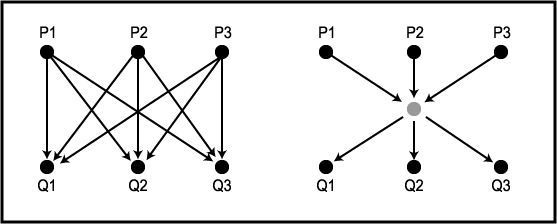
그림 3 두 개의 네트워크 - 하나는 은닉변수 포함
때로는 훈련 집합 Ξ에 서 값이 주어지지 않은 변수를 표현하는 노드를 네트워크에 추가함으로써 네트워크 구조를 상당히 단순화시킬 수 있다. 이런 노드를 은닉 노드 (hidden node) 라 한다. 간단한 예로 그림 3 에 있는 두 개의 베이지안 네트워크를 고려하자. 왼쪽에 있는 네트워크가 오른쪽에 은닉노드 H 를 포함한 네트워크보다 더 많은 매개변수를 가지고 있고, 따라서 만일 오른쪽 네트워크의 데이터 적합도가 왼쪽 네트워크보다 같거나 더 좋다면 (변수 사이의 내재된 인과관계를 더 잘 표현한다면) 왼쪽 네트워크의 코드길이 점수가 더 나쁠 것이다. 은닉변수는 측정할 수 있는 것이 아니므로 탐색 과정에서 만들어내야 한다. 이를 위해서는 탐욕 탐색을 할 때 가능한 변화 리스트에 새로운 노드의 추가를 추가해야 한다 ([Heckerman 1996] 을 참조하라). 대응되는 변수의 값은 물론 결여된 데이터이고 이 변수와 연관된 확률은 앞에서 기술한 대로 EM 방법에 의해 제시되어야 한다.
2. 확률 추론과 행동
2.1 일반 설정
확률 추론을 이용하는 많은 응용이 있다. 그 중에서 두드러진 것은 특정 데이터에 적용되는 일반 지식을 바탕으로 가장 적절한 추측을 하는 저문가 시스템에서 찾아볼 수 있다. 주어진 증상에 대해 질병의 상태를 진단하는 것이 한 예가 된다. 여기서는 에이전트가 주어진 감지 정보와 환경 상태의 평가 척도를 바탕으로 가장 적절한 다음 행동을 결정해야 할 때, 베이지안 네트워크를 이용한 확률 추론을 어떻게 적용하는지를 기술하고자 한다 (여기서는 다루는 방법은 [Russell & Norvig 1995 의 17장] 에 기반을 두고 있으며, [Dean & Wellman 1991 의 7장] 의 방법도 기술한다).
여기서 다루고자 하는 문제는 계획, 행동 그리고 학습에서 이미 도전했던 문제를 일반화한 것이다. 그때 감지/계획/행동 주기 (sense/plan/act cycle) 를 이용한 에이전트에 대해 기술했던 것을 기억할 것이다. 계획 단계에서는 목적을 향해 몇 단계 내다보는 방법을 이용하여 현재 환경 상황에서 취해야 할 가장 적절한 다음 행동을 계산하였다. 행동 단계에서는 계획자가 추천한 맨 처음 행동을 수행하였고, 감지 단계는 다음 주기를 위해 결과로 나타나는 환경 상황을 인식하였다. 계획, 행동 그리고 학습에서는 또한 목표 (goal) 의 개념을 특정한 환경 상태에서 주어지는 (또는 빼앗는) 보상 목록 (schedule of rewards) 이란 것으로 일반화시켰다. 이 보상은 다시 각 상태에 대해서 어떤 "값" 을 이끌어내는데, 이 값은 에이전트가 보상을 최대화하기 위해 행동하여 얻을 수 있는 총 할인된 추후 보상 (future reward) 으로 나타낸다. 여기서는 효용성 (utility) 이 각 환경 상태에서 기인한다고 보고 이러한 일반화된 목표의 개념을 계속 유지하고자 한다.
이전에 기술한 감지/계획/행동 에이전트의 구조에서는 환경에 대한 가정이나 감지와 행동의 신뢰성에 대한 가정이 다소 일관적이지 못하였다. 즉, 에이전트가 감지 작업을 통해서 현재 상태를 정확히 결정할 수 있고 모든 행동의 결과를 정확히 예측할 수 있다고 가정하였다. 하지만 이러한 가정이 맞지 않는 경우 (일반적으로 맞지 않음), 에이전트는 단일 행동을 취하고 바로 센서를 이용하여 환경 상태가 실제로 어떻게 바뀌었는지를 파악하였다. 이 접근 방법을 합리적으로 다루기 위해, 수행한 행동이 항상 예측된 결과를 내지 않거나 센서가 가끔 행동 오류를 일으키더라도 센서가 에이전트에게 상태공간에서의 진행 상황을 알려주고 반복적으로 계획수립을 하여 에이전트가 요구하는 목적 (또는 보상) 을 향해 갈 수 있도록 방향을 재조정하도록 하였다.
이제 불확실성을 적절히 다룰 수 있는 도구가 마련되었기 때문에 명시적으로 좀 더 현실적인 가정을 채택할 수 있다. 새로운 에이전트는 자신이 어떤 상태에 있는지 알기보다는 자신이 여러 다양한 상태에 대해 놓일 수 있는 확률만을 알게 된다. 그리고 환경 상태에 대한 정확한 지식을 주는 센서 대신에 에이전트의 센서는 이러한 확률을 다듬어주는 정도의 일을 할 뿐이다. 행동의 결과는 막연하게만 알 수 있는데, 주어진 상태에서 취한 행동의 결과는 새로운 상태의 집합에 있는 어떤 상태도 될 수 있으며 각 상태마다 확률이 연관되어 있다. 계획 수립과 감지 작업을 통해서 에이전트가 효용성의 기대값을 최대화하는 행동을 선택할 수 있도록 하고자 한다. 에이전트가 이러한 문제를 완전히 일반화시켜 다룰 수 있도록 하려면 매우 많은 계산이 필요하기 때문에 근사치 계산이나 다른 제한적인 가정을 해야 한다. 이러한 내용에 대해 다음 절에서 예제를 들어 논의하고자 한다.
2.2 확장된 예제
앞에서 논의되었던 가정을 바탕으로 작업할 경우 계산이 매우 어려워지기 때문에, 이 예제에서는 아주 간단한 에이전트와 환경을 이용해서 주된 아이디어를 희석시키지 않게 하려고 한다. 가령 그림 4 에서와 같이 5 개의 셀로 구성된 1 차원 격자 (grid) 에 존재하는 로봇을 고려하자. 이 경우 환경 상태는 로봇의 위치만을 포함하며, 이것은 {-2, -1, 0, 1, 2} 의 5 개의 가능한 값을 갖는 상태변수 E 로 나타낸다. 각 위치는 로봇에 대한 효용값 (utility) U 를 가진다. 가운데 셀은 효용값이 0 이며, 이러한 효용값들을 그림에 나타내었다. 초기에는 로봇이 t = 0 인 시간에 자신이 0 으로 표시된 셀에 있다는 것을 (정확히) 안다고 가정한다. 즉, E0 = 0 이다.
그림 4 5 개의 셀에 갇힌 로봇
i 번째 시점에서 로봇이 취하는 행동은 Ai 의 기호로 나타낸다. 로봇은 왼쪽으로 한 셀만큼 이동 (Ai = L) 하거나 오른쪽으로 한 셀만큼 이동 (Ai = R) 할 수 있다. 어느 경우이건 한 번 이동하여 의도된 결과가 나올 확률은 0.5 이고, 각 행동의 결과로 아무 변화가 없을 확률은 0.25 이며, 한 행동이 로봇을 의도된 방향과 반대 방향에 있는 인접셀로 이동하게 할 확률은 0.25 이다. 따라서, 처음 몇 번을 움직이고 나면 로봇은 자신의 실제 위치에 대한 확률 지식만을 가지게 된다.
로봇은 감지신호 Si 를 통해 i 번째 시점에서의 자신의 위치를 감지한다. 하지만 센서가 다소 신뢰성이 없다고 가정한다. 즉, Ei 가 어떤 값을 가질 때, Si 가 같은 값을 가질 확률을 0.9 로 하고, 다른 값 4 가지 중 하나일 확률은 0.025 이다.
이 로봇에서의 문제는 여러 불리한 조건에 직면했을 때 몇 단계 앞을 내다보고 효용성의 기대값이 최대가 되도록 이동하는 것이다. 로봇의 다음 행동을 선택할 때 이용되는 결정 기법은 한 단계만 내다 본 효용값 기대치의 최대화를 통해 아주 쉽게 설명될 수 있다. 로봇이 t = 0, 즉 A0 = R 일 때 오른쪽으로 이동하려 한다고 하자. 이 행동의 결과로 얻어지는 환경 상태는 Ei 이 된다. 이 로봇이 감지/계획/행동의 주기를 계속하면 자신의 위치를 예를 들어 Si = 1 이라고 감지하게 된다. 다음은 어디로 이동해야 하는가? 이렇게 이동한 후에는 감지된 데이터를 바탕으로 한 이동이나 현재 위치에 대한 추론, 그리고 행동의 결과를 어떻게 지속적으로 선택할 수 있는가?
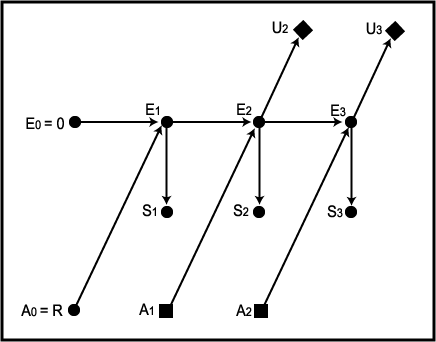
그림 5 동적결정 네트워크
동적 결정 네트워크 (dynamic decision network) 라 부르는 특수한 형태의 믿음 네트워크 (belief network) 를 이용하는 확률 추론은 효용성을 최대화하는 행동을 선택하기 위해 사용될 수 있다. 이 문제에 적합한 네트워크를 그림 5 에 나타내었다. 이 네트워크는 행동이 취해지고 새롭게 감지된 정보가 있을 때마다 로봇이 반복적으로 추론을 할 수 있도록 해준다. E0 = 0, A0 = R, Si = 1 의 값이 주어지면 통상적인 확률 추론을 이용해서, A1 = R 과 A1 = L 로부터 얻을 수 있는 효용값 기대치인 U2 를 계산한다. 그리고 나서 로봇은 이 중 더 큰 값을 주는 행동을 선택한다 [아 경우 행동의 선택은 한 번의 이동만 내다본다. 더 많이 예견하게 되면 일련의 대안 행동 (alternative action sequence) 에 대한 원거리 효용값 (distant utility) 을 더 많이 계산해야 한다]. 동적결정 네트워크에서는 서로 다른 가정을 갖는 노드를 구별하기 위해 다른 모양의 노드를 이용한다. 상자모양의 노드 (■) 는 여전히 에이전트에 의해 값이 제어되는 변수를 가리킨다. 이런 노드를 결정 노드 (decision node) 라 한다. 동적 결정 네트워크에서 에이전트가 이 노드를 선택한 후에는 이 노드는 통상적인 믿음 네트워크 노드 (값이 알려진) 가 된다. 다이아몬드 모양의 노드 (◆) 는 효용값을 나타내는 변수를 가리킨다. 효용성 변수의 기대값은 여러 가지 부모값들의 확률에 대한 함수이다.
네트워크 구조를 보면 환경이 마르코프 환경인 것을 알 수 있다. 즉, 시간 t + 1 일 때의 환경 상태는 (감지하지 않고도) 시간 t 일 때의 환경 상태와 행동에 의해서 (확률적으로) 완전 결정된다. 이런 측면에서 대부분의 에이전트 환경이 마르코프 환경이라고 가정할 수 있다 (추가 변수를 도입하여 마르코프 환경을 만들 수도 있다). 또한 이 네트워크의 구조는 시간 t 에서의 환경에 대해 t 에서 감지된 것은 그 전에 감지된 모든 것과 조건부 독립적이라는 가정을 내포한다.
t = 1 일 때 계획된 (효용값 기대치인 U2 를 최대화하는 과정을 거쳐 계획이 수립된) 행동을 취하여 시점을 하나 앞으로 이동시키고 다음 상태인 E2 에서 S2 를 감지한 후에는 또 다른 감지/계획/행동의 주기를 가지고 전체 과정이 반복된다. 필요한 계산 중 일부를 직접 해보는 것이 도움이 될 것이다.
먼저, A1 에 대한 서로 다른 두 가지 확률을 가정하여, 시간 t = 0 에서 알려진 것에 대한 두 개의 효용값 기대치를 계산해야 한다.
Ex [U2 | E0 = 0, A0 = R, S1 = 1 , A1 = R]
Ex [U2 | E0 = 0, A0 = R, S1 = 1 , A1 = L]
이 기대값을 구하기 위해서는 A1 의 두 값의 각각에 대해서 E2 의 여러 값에 대한  (E2 | E0 = 0, A0 = R, S1 = 1 , A1) 을 계산해야 한다. 이러한 형태의 계산은 나중 단계에서도 반복되지만 구체화하기 위해 현 단계에 대해서 수행하고자 한다. 이 형태는 A1 의 각 값에 대해 동일하기 때문에 A1 = R 일 경우만 구하면 된다. 앞장에서 설명한 다중트리 (polytree) 알고리즘을 이용하여
(E2 | E0 = 0, A0 = R, S1 = 1 , A1) 을 계산해야 한다. 이러한 형태의 계산은 나중 단계에서도 반복되지만 구체화하기 위해 현 단계에 대해서 수행하고자 한다. 이 형태는 A1 의 각 값에 대해 동일하기 때문에 A1 = R 일 경우만 구하면 된다. 앞장에서 설명한 다중트리 (polytree) 알고리즘을 이용하여  (E2 | E0 = 0, A0 = R, S1 = 1, A1 = R) 을 계산해 보자.
(E2 | E0 = 0, A0 = R, S1 = 1, A1 = R) 을 계산해 보자.
먼저, "값이 주어지지 않은 부모를 포함시켜" 다음을 얻는다.
 (E2 | E0 = 0, A0 = R, S1 = 1, A1 = R)
(E2 | E0 = 0, A0 = R, S1 = 1, A1 = R)
= 
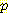 (E2 | A1 = R, E1)
(E2 | A1 = R, E1) 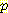 (E1 | E0 = 0, A0 = R, S1 = 1)
(E1 | E0 = 0, A0 = R, S1 = 1)
로봇의 행동을 선택하기 위해 사용되는 결정 네트워크에서는 이 합산 공식의 첫 번째 항을 마르코프 프로세스의 행동 모델 (action model) 이라 한다. 이 모델은 바로 전의 상태와 행동이 주어졌을 때 가능한 여러 가지 다음 상황에 대한 확률을 나타낸다. 다중트리 알고리즘에 따르면 이 합산 공식의 두 번째 항은 베이지안 규칙을 이용하여 다음과 같이 다시 쓸 수 있다.
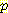 (E2 | E0 = 0, A0 = R, S1 = 1) =
(E2 | E0 = 0, A0 = R, S1 = 1) = 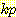 (S1 = 1 | E1)
(S1 = 1 | E1) 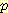 (E1 | E0 = 0, A0 = R)
(E1 | E0 = 0, A0 = R)
이 곱셈에서 첫 번째 항을 센서 모델 (sensor model) 이라 한다. 이 모델은 임의의 환경 상황에 대해서 센서가 여러 값을 가질 확률을 나타낸다 (완전히 신뢰할 수 있고 매우 유익한 센서라면 모든 확률을 구할 때 각 환경 상태에 대해서 하나의 센서값에만 집중할 것이다). 두 번째 항은 앞에서와 같이 행동 모델이 된다.
이 결과들을 모으면 다음과 같다.
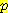 (E2 | E0 = 0, A0 = R, S1 = 1, A1 = R)
(E2 | E0 = 0, A0 = R, S1 = 1, A1 = R)
= 
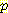 (E2 | A1 = R, E1)
(E2 | A1 = R, E1) 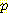 (S1 = 1 | E1)
(S1 = 1 | E1) 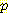 (E1 | E0 = 0, A0 = R)
(E1 | E0 = 0, A0 = R)
이 표현식을 (E2 의 여러 값에 대해) 계산하기 위해 행동의 결과와 센서의 신뢰성에 대해 내렸던 확률가정을 이용한다. 이를 시연하기 위해 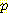 (E2 = 1 | E0 = 0, A0 = R, S1 = 1, A1 = R) 만을 계산해 보자. 이 계산은 다음과 같은 확률을 포함하며 이 확률은 그림 5 에 있는 네트워크에 대한 CPT 의 항목으로 들어가게 된다 (모든 E1 값에 대해 합산을 해야 한다).
(E2 = 1 | E0 = 0, A0 = R, S1 = 1, A1 = R) 만을 계산해 보자. 이 계산은 다음과 같은 확률을 포함하며 이 확률은 그림 5 에 있는 네트워크에 대한 CPT 의 항목으로 들어가게 된다 (모든 E1 값에 대해 합산을 해야 한다).
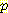 (E2 = 1 | A1 = R, E1 = 0) = 0.5
(E2 = 1 | A1 = R, E1 = 0) = 0.5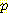 (E2 = 1 | A1 = R, E1 = 1) = 0.25
(E2 = 1 | A1 = R, E1 = 1) = 0.25 (E2 = 1 | A1 = R, E1 = 2) = 0.25
(E2 = 1 | A1 = R, E1 = 2) = 0.25 (E2 = 1 | A1 = R, E1 = -1) 와
(E2 = 1 | A1 = R, E1 = -1) 와  (E2 = 1 | A1 = R, E1 = -2) 는 모두 0
(E2 = 1 | A1 = R, E1 = -2) 는 모두 0 (S1 = 1 | E1 = -2) = 0.025
(S1 = 1 | E1 = -2) = 0.025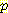 (S1 = 1 | E1 = -1) = 0.025
(S1 = 1 | E1 = -1) = 0.025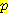 (S1 = 1 | E1 = 0) = 0.025
(S1 = 1 | E1 = 0) = 0.025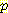 (S1 = 1 | E1 = 1) = 0.9
(S1 = 1 | E1 = 1) = 0.9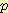 (S1 = 1 | E1 = 2) = 0.025
(S1 = 1 | E1 = 2) = 0.025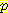 (E1 = -1 | E0 = 0, A0 = R) = 0.25
(E1 = -1 | E0 = 0, A0 = R) = 0.25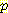 (E1 = 0 | E0 = 0, A0 = R) = 0.25
(E1 = 0 | E0 = 0, A0 = R) = 0.25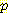 (E1 = 1 | E0 = 0, A0 = R) = 0.5
(E1 = 1 | E0 = 0, A0 = R) = 0.5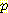 (E1 = -2 | E0 = 0, A0 = R) 와
(E1 = -2 | E0 = 0, A0 = R) 와 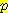 (E1 = 2 | E0 = 0, A0 = R) 는 모두 0
(E1 = 2 | E0 = 0, A0 = R) 는 모두 0
합산을 하면 다음과 같이 된다.
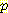 (E2 = 1 | E0 = 0, A0 = R, S1 = 1, A1 = R)
(E2 = 1 | E0 = 0, A0 = R, S1 = 1, A1 = R)
= 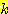 × [(0.5 × 0.025 × 0.25) + (0.25 × 0.9 × 0.5)]
× [(0.5 × 0.025 × 0.25) + (0.25 × 0.9 × 0.5)]
= 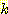 × 0.14375
× 0.14375
E2 의 다른 값에 대한 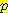 (E2 | E0 = 0, A0 = R, S1 = 1, A1 = R) 를 구하기 위해서도 유사한 계산을 수행한다. 이 모든 확률의 합은 1 이므로
(E2 | E0 = 0, A0 = R, S1 = 1, A1 = R) 를 구하기 위해서도 유사한 계산을 수행한다. 이 모든 확률의 합은 1 이므로 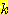 를 구할 수 있다. E2 에 대한 이 확률을 이용해서 A1 = R 일 때의 U2 의 기대치를 계산하게 된다. 이 과정을 반복하여 A1 = L 일 때 U2 의 기대치를 계산하고 그 중 큰 값을 가지는 행동을 선택하게 된다 (이 문제의 구조로 볼 때 A1 = R 의 행동이 선택될 것이 당연하지만 방법을 설명하기 위해 이 예제를 이용하였다)
를 구할 수 있다. E2 에 대한 이 확률을 이용해서 A1 = R 일 때의 U2 의 기대치를 계산하게 된다. 이 과정을 반복하여 A1 = L 일 때 U2 의 기대치를 계산하고 그 중 큰 값을 가지는 행동을 선택하게 된다 (이 문제의 구조로 볼 때 A1 = R 의 행동이 선택될 것이 당연하지만 방법을 설명하기 위해 이 예제를 이용하였다)
2.3 예제의 일반화
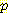 (E2 | E0 = 0, A0 = R, S1 = 1, A1 = R) 에 대한 공식을 분석해 보면 이 공식을 차후의 시점으로 확장할 수 있다는 것을 알 수 있다. 이 공식은 시간 t = 1 에서 S1 = 1 이 감지되고 나서 A1 = R 의 행동이 취해지기 전에 계산된다. 따라서 위의 공식 대신에
(E2 | E0 = 0, A0 = R, S1 = 1, A1 = R) 에 대한 공식을 분석해 보면 이 공식을 차후의 시점으로 확장할 수 있다는 것을 알 수 있다. 이 공식은 시간 t = 1 에서 S1 = 1 이 감지되고 나서 A1 = R 의 행동이 취해지기 전에 계산된다. 따라서 위의 공식 대신에 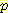 (E2 | <values before t = 1>, S1 = 1, A1 = R) 과 같이 쓸 수 있다. 이와 비슷하게 합산 공식에서의
(E2 | <values before t = 1>, S1 = 1, A1 = R) 과 같이 쓸 수 있다. 이와 비슷하게 합산 공식에서의 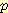 (E1 | E0 = 0, A0 = R) 의 표현식은
(E1 | E0 = 0, A0 = R) 의 표현식은 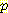 (E1 | <values before t = 1>) 과 같이 쓸 수 있다. 이러한 변경을 고려하면 다음과 같은 식을 얻는다.
(E1 | <values before t = 1>) 과 같이 쓸 수 있다. 이러한 변경을 고려하면 다음과 같은 식을 얻는다.
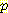 (E2 | <values before t = 1>, S1 = 1, A1)
(E2 | <values before t = 1>, S1 = 1, A1)
= 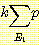 (Ei+1 | Ai, Ei)
(Ei+1 | Ai, Ei)  (Si = si | Ei)
(Si = si | Ei)  (Ei | <values before t = i>)
(Ei | <values before t = i>)
행동에 대한 결정을 내리기 위해서는 시간이 경과할 때마다 다음과 같은 방법으로 이 공식을 이용한다. 시간 t = i 에서 취할 A1 의 행동을 계산하기 위해서는 다음과 같이 한다.
|
1. 바로 전인 (i - 1) 시점으로부터 (그리고, Si-1 = si-1 을 감지한 후), 이미 Ei 의 모든 값에 대해 2. 시간 t = i 에서 Si = si 를 감지하고 센서 모델을 이용해서 Ei 의 모든 값에 대해 3. 행동 모델로부터 Ei 와 Ai 의 모든 값에 대해 4. Ai 의 각 값과 Ei+1 의 특정값에 대해 5. 바로 전 단계를 Ei+1 의 모든 값에 대해 반복하여 Ei+1 과 A i 의 각 값에 대해 6. 이 확률값들을 이용해서 Ai 의 각 값에 대한 Ui+1 의 기대치를 계산하고 기대치를 최대화하는 Ai 를 선택한다. 7. 이전 단계에서 선택된 행동을 수행하고, i 를 하나 증가시킨 후 위 과정을 반복한다. |
이것이 바로 동적 결정 네트워크를 이용해서 행동을 선택하는 핵심 과정이다. 이 방법은 위와 같은 쉬운 예제 이상의 예제에도 확장된다. 행동이 환경에 미치는 영향이나 환경이 센서 자극에 미치는 영향들은 일반적으로 그림 5 와 유사한 네트워크를 이용하여 잘 모델링될 수 있다. 각 시점에서 단일 환경변수인 Ei 대신에 값 벡터인 Ei = (Ei1, ..., Ein) 을 이용할 수 있다. 이와 비슷하게, 단일 감지변수인 Si 대신에 값 벡터인 Si = (Si1, ..., Sim) 을 이용할 수 있다. 물론 각 시점에서의 동적 결정 네트워크는 이런 모든 변수와 종속성에 대한 노드를 포함시킬 수 있도록 확장되어야 하지만, 일반적인 계산 형태는 앞에서 간단한 예제에 대해 한 것과 동일하다. 주어진 시점에서 내부적인 네트워크가 복잡하더라도 마르코프의 가정은 시점 사이의 종속성을 단순화시킨다.
한 단계 이상을 내다보려면 확률을 효용값 기대치가 계산되는 지점까지 전달해야 한다. 당연히 이러한 확장은 금새 비현실적인 것으로 나타난다. 더구나 Ei 에 대한 확률 분포가 매우 광범위하게 흩어질 수 있기 때문에 유용성도 떨어진다. 따라서 이러한 확률적 확장을 제안하기 전에 언급했던 다소 일관성이 없는 가정을 포함하는 절충 방법이 합리적인 대안이 될 수 있다.
3. 참고문헌 및 토론
베이지안 네트워크에 대한 학습은 매년 새로운 중요한 논문이 발표되는 활발한 연구 분야이다. [Neal 1991 (Neal, R., "Connectionist Learning Of Belief Networks," Artificial Intelligence, 56:71-113, 1991.)] 은 신경망을 이용해서 베이지안 네트워크를 학습하는 방법을 기술하였다. 제시된 베이지안 네트워크 구조를 평가하기 위해 이 책에서 기술된 기법은 최소 코드길이 [Rissanen 1984 (Rissanen, J., "Universal Coding, Information, Prediction, and Estimation," IEEE Transactions on Information Theory, IT-30(4):629-636, 1984.)] 의 개념을 이용하였다. [Friedman 1997 (Friedman, N., "Learning Belief Networks in the Presence of Missing Values and Hidden Variables," Proceedings of the Fourteenth International Conference on Machine Learning (ICML '97), San Francisco: Morgan Kaufmann, 1997.)] 은 네트워크의 구조를 알지 못하고 결여된 데이터가 존재할 경우에 베이지안 네트워크를 학습하는 기법을 기술하였다. 베이지안 네트워크의 학습에 대한 초기 연구는 [Cooper & Herskovitz 1992 (Cooper, G., and Herskovitz, E., "A Bayesian Method for the Induction of Probabilistic Networks 'from Data," Machine Learning, 9:309-347, 1992.)] 에 의해 이루어졌다.
[Forbes, et al. 1995 (Forbes, J., Huang, T., Kanazawa, K., and Russell, S., "The BATmobile: Towards a Bayesian Automatic Taxi," in Proceedings of the Fourteenth International Joint Conference on Artificial Intelligence (IJCAI-95), pp.1878-1885, San Francisco: Morgan Kaufmann, 1995.)] 는 동적 결정 네트워크를 이용해서 자동차를 운전하는 시스템을 제시하였다.
확률적 상황 (stochastic situation) 에서의 효용성 평가는 결정론 (decision theory) 분야의 주된 관심사이다. AI 에서 결정론의 이용을 어떻게 다루는지를 보려면 [Horvitz, Breese, & Henrion 1988 (Horvitz, E., Breese, J., and Henrion, M., "Decision Theory in Expert Systems and Artificial Intelligence," International Journal of Approximate Reasoning, 2:247-302, 1988.)]을 참조하라. 마르코프 결정 문제 (Markov decision problems, MDPs) [Puterman 1994 (Puterman, M., Markov Decision Processesm Discrete Stochastic Dynamic Programming, New York: John Wiley & Sons, 1994.)] 에 대한 이론과 부분적으로 관찰 가능한 마르코프 결정 문제 (partially observable MDPs, POMDPs) [Cassandra, Kaelbling, & Littman 1994 (Cassandra, A., Kaelbling, L., and Littman, M., "Acting Optimally in Partially Observable Stochastic Domains," in Proceedings of the Twelfth National Conference on Artificial Intelligence (AAAI-94), pp.1023-1028, Menlo Park, CA: AAAI Press, 1994.)] 에 대한 이론은 확률적 상황에서 행동의 결과에 대한 기본적 이론 모델을 제공한다.
 (Ei | <values before t = 1>) 를 계산하였다.
(Ei | <values before t = 1>) 를 계산하였다. (Si = si | Ei) 를 계산한다.
(Si = si | Ei) 를 계산한다. (Ei+1 | Ai, Ei) 를 계산한다.
(Ei+1 | Ai, Ei) 를 계산한다. (Ei+1 | Ai, Ei)
(Ei+1 | Ai, Ei)  (Si = si | Ei)
(Si = si | Ei)  (Ei | <values before t = i>) 의 곱을 Ei 의 모든 값에 대해 더하고, 상수
(Ei | <values before t = i>) 의 곱을 Ei 의 모든 값에 대해 더하고, 상수  를 곱해서
를 곱해서  (Ei+1 | <values before t = i>, Si = si | A i) 에 비례하는 값을 얻는다.
(Ei+1 | <values before t = i>, Si = si | A i) 에 비례하는 값을 얻는다. (Ei+1 | <values before t = i>, Si = si | A i) 의 실제 값을 얻을 수 있도록 상수
(Ei+1 | <values before t = i>, Si = si | A i) 의 실제 값을 얻을 수 있도록 상수  를 계산한다.
를 계산한다.